C6
Hybrid model for the boundary surface between a packed bed and the downstream free flowing gas
Principal Investigator
Doctoral candidate
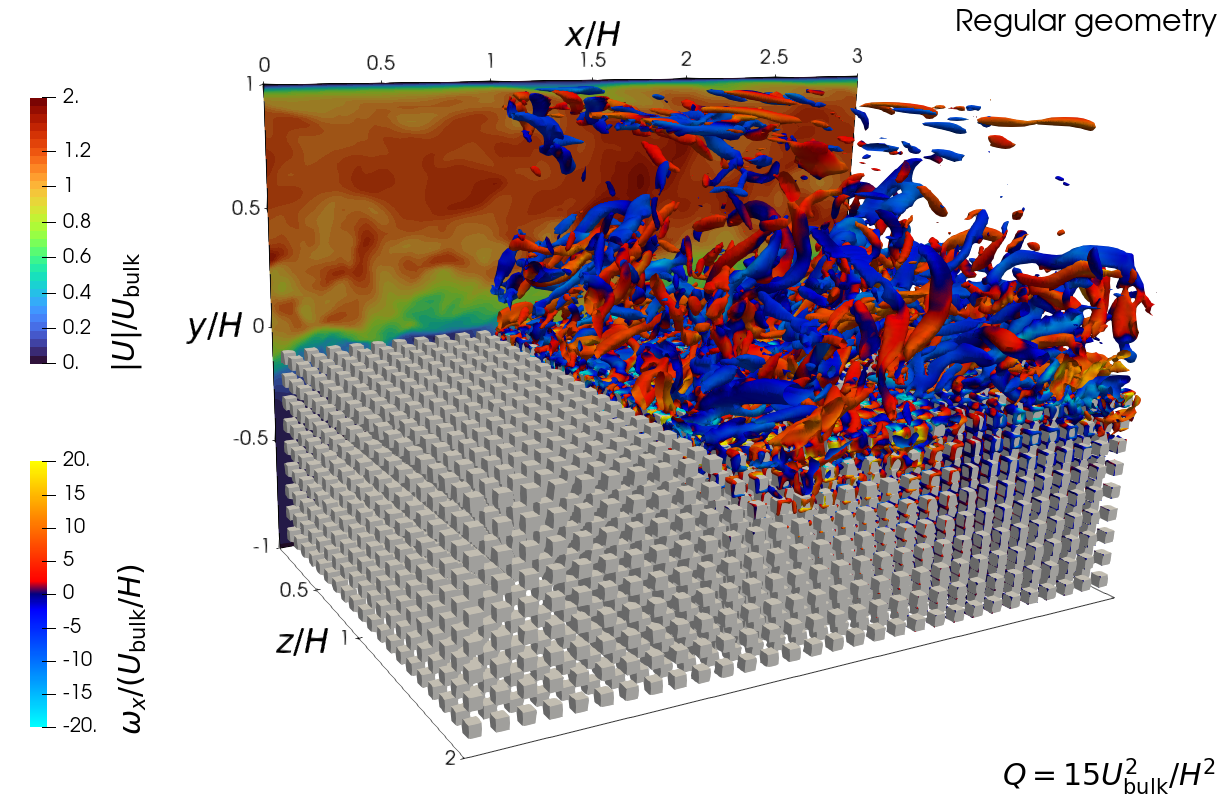
Figure 1. The turbulent flow through the channel half-filled with porous medium, modelled by an array of cubes. The fluctuating velocity field is visualised in a part of the domain by the iso-surfaces of second invariant of the velocity gradient tensor coloured by the streamwise vorticity. Magnitude of the instantaneous velocity field is visible at the plane behind the vortices.
In project C6 the large eddy simulation approach will be employed to derive a seamless model of the bed’s free surface in the form of source, respectively sink, terms, to be included in classic RANS simulations, thus correctly accounting for the mixing processes at the interface between the packed bed and the free gas phase. The interface between the dense bed of chemical reacting particles and the gas phase freeboard (free gas phase) downstream of the bed needs special treatment. This is especially always the case when the particles release volatile hydrocarbons, H2 or CO which mix and can react at least partially in the bed but also, for example, in a free gas flame, downstream of the bed together with the air passing which flows through the bed (e.g. volatiles flame downstream of a bed of Pellets on a grate). Hence, it is of paramount importance to gain a better understanding of the transport mechanisms of micro-scale turbulence into the freeboard region, as this is likely to strongly influence scalar mixing and therefore chemical reaction.
In funding period (FP) 1, project C6 will focus on packed beds accounting for spherical, non-reacting particles and the freeboard region above the bed. The system of Navier-Stokes equations and appropriate scalar conservation equations will be analysed in the light of first principles and a spatial filtering operator will be defined and applied, such that both the flow field realised in the interstices among the solid particles and the flow in the free gas phase will be encompassed, accurately accounting for the morphology of the packed bed as well as the nature and shape of the particles. The unclosed terms arising from the filtering of the governing equations must vanish identically in case of a fully resolved simulation (Direct Numerical Simulation). This principle will guide the successive steps of the research.The configuration measured in project A1 (Zähringer/Lessig) will be simulated and reference data generated, which will serve a twofold purpose. Firstly, the governing equations will be subjected to filtering and the resulting unclosed terms will be computed exactly a priori from the resolved simulation. Based on this step, functional expression for appropriate closures will be derived. A mathematical quantification of the modelling errors will be also obtained by means of analytical LES-quality criteria. Furthermore, the configuration will be employed to validate the additional, modelled terms appearing in the system of filtered equations in the context of under-resolved simulations such as RANS and VLES. The closures derived in project C6 for the dispersion and cross stresses and scalar fluxes at the bed’s free surface will be then made available to project C7 (Scherer/Wirtz).
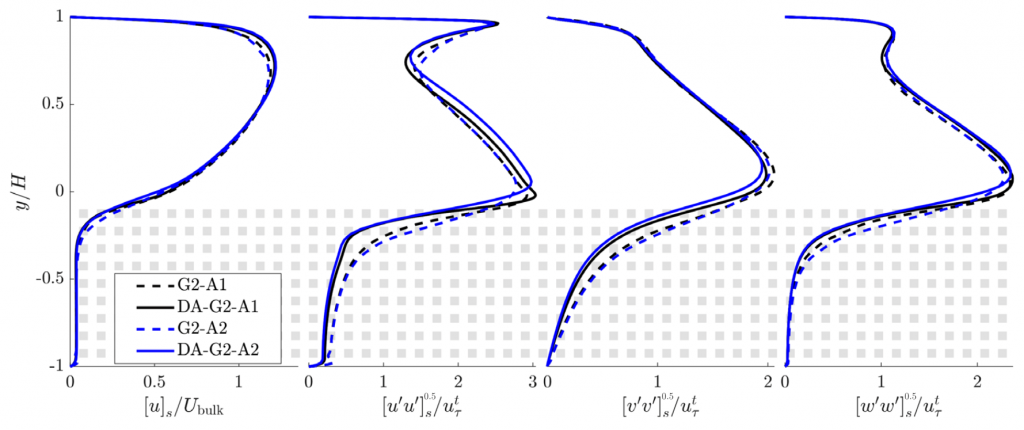
Figure 2. Comparison of double-averaged (in time and filtered in space) streamwise velocity and rms of turbulent fluctuations between the particle resolved, large eddy simulation of the channel (dashed lines) and similar configuration using macroscopic model of the particles. Blue lines and black lines denote different filter sizes (black: characteristic filter size two times greater than the cube size, blue: four times greater).
To formulate successful and accurate closure models for the various variables resulting from up-scaling (filtering in space) the flow in the particle assemblies, the properties of filtered equations need to be closely examined. In project C6 the Double-Averaged Navier-Stokes (DANS) equations have been rederived assuming spatial filtering with a chosen kernel function instead of standard volume averaging approach. Additionally, the filtering approach has been extended to include the case of filter size changing in space, which is formally required of large eddy simulation coupled with up-scaled model of the bulk. Furthermore, the equations have been analysed from the point of view of interface modelling and tested by conducting a large eddy simulation in a channel half-filled with arrays of cubes, which was modelled as a porous medium. The results were in a good agreement with the data obtained from particle resolved simulation of the same configuration, showcasing the applicability of DANS system.



